N-Queens problem is defined as: place n queens on an \(n × n\) chess board so that the queens do not attack each other. Now, we rotate the board clockwisely by 45 degrees as shown in following picture, and use a variable to denote the queen partition (if any) for each row (a diagonal in the original board).

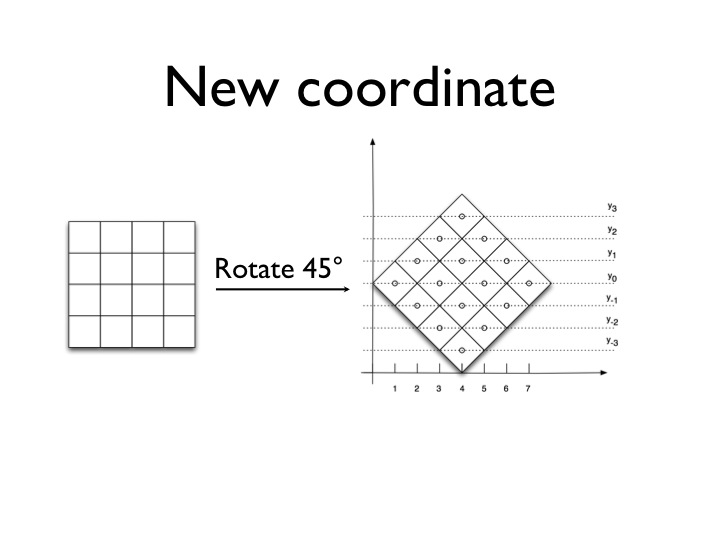
Thus the variables are \(y_{1-n}, y_{2-n},..., y_{0},..., y_{n-2}, y_{n-1}.\) While each variable takes values according to the new coordinate system, we use the value \(−n\) to denote that there are no queens on a particular row. The domain of each variable \(y_i\) is thus \(D_i = { |i|+1,|i|+3,...,2n−|i|−1 } ∪ {−n}\) for \(i \in [1−n,n−1]\). The set of constraints are given as follows:

• for \(i \in [1−n,n−1]: \sum_i(y_i \ne −n)=n\)
• for \(i \in [1−n,n−1]\) and \(j \in [1,2n−1]: \sum_i(y_i =j) \leq 1\)
• for \(i,j \in [1−n,n−1]\) and \(i \ne j:|y_i−y_j| \ne |i−j|\)

The model is modeled in three ways: arithmetic constraint, tuple sets and DFA.

The Gecode implementation has been uploaded to my github repository. You can see the source code at wangdaiwei/gecode.

The program should be run as following command in Mac OSX:

queens -model mod 5

Here mod stands for the model you choose. The value is from 1 to 3. The last parameter defines the size of N-Queens problem.