这篇文章来自Alan Zucconi的博客,原文链接: http://www.alanzucconi.com/2016/08/17/fractals-101/
Alan还写了很多关于Unity教程的博客,写的都非常好,推荐大家去看一下。
这个系列的教程将会解释分形这个概念,为什么它很重要以及我们能够从中学到什么。本文将浅要地概述迭代分形和分形维度的概念。
分形这个概念在自然界中很常见,因此这个系列非常适合那些想在游戏里模拟一个真实的户外环境的人,包括所有的美术和游戏开发人员。
简介
拿我们非常熟悉的球体举例,平时我们观察球体时觉得它的面是一个曲面,如果你以非常近的距离观察球体,你会发现当距离足够近的时候,整个球面就好像平面一样。这种情况就好像我们每天观察地球一样,我们生活的地方看上去就是一个很大的平面,但实际上地球是圆的。除了地球,其他任何形状的物体也是一样,即使是最精细的多面体,离得足够近时也依然是平面构成的。简而言之,所谓球体这个概念,只有在一定距离观察才有意义。这个概念如此的显而易见,似乎我们可以认为所有物体应该都有这样的特性。但还是有一些特别的几何体超出了这个概念的范围,这种特殊的形状能够包含无限层次的精细程度,我们称之为分形。这种物体具有一种奇特的特征,不管我们以多么近的距离去观察它,它的细节程度丝毫不会损失,反而会越来越精细。更为奇特的是,有一些分形会具有一种叫做自相似性的属性,观察某一部分的细节时,会发现这一部分具有跟整体一样的复杂度。这种图形就类似于无穷迭代,你凑近一点看,发现这是一个三角形,你往某一个角上使劲观察,会发现它还是个三角形,子子孙孙无穷匮也。
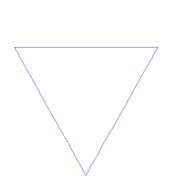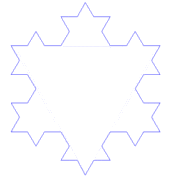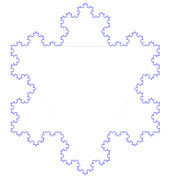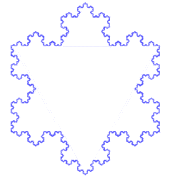
这段动画演示的是科赫曲线,一个非常简单的分形的例子。它是分步创建的,每一次循环都添加了额外的复杂度。第一步是创建一个三角形,接下来的每一步都用到了上一步创建的三条边,并给每一条边放置一个三角形,创建出一个六角星的形状。只有是无限迭代生成的曲线才能够称作是完整的科赫曲线。很明显的,它的细节是无限的,每一个循环都在增加它的复杂度,每一个循环都在一定程度上扩展了曲线的周长,因此完整的科赫曲线具有无限的周长。
分形的维度
之所以叫做分形,是有一定道理的。不过了解这一点之前,我们先来看看维度的概念。我们都很熟悉线是1维的,平面是2维的,而具有体积的物体是3维的。但是为什么线是1维的呢?原因是对于1维的物体而言,任何一个点在1维的中都只需要一个数字来表示。你可以想象一下这样一个场景:你住在一个街上,每一个房子都有一个唯一的房号标识,这个标号可以是这么计算的,是房子到这条街的开始位置的位置。因此给出一个固定的原点,每一个1维的线上都能用到原点的距离表示。
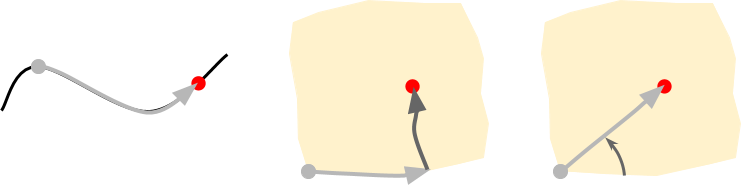
对于2维的形状也是如此,这时需要用两个坐标来表示每一个点的位置。不管是处在笛卡尔坐标系还是极坐标系,都需要用到两个数字来表示位置。
回头再来看看上一节介绍的科赫曲线,我们希望它能够像1维的物体一样,毕竟它是由线条构成的。然而,对于科赫曲线上的点而言,一个坐标并不足以表示曲线上的点,因为在科赫曲线上的任意两点的距离都是相同的:无穷大,可是它也不是2维的,因为它并没有面积的概念。实际上,它的维度介于1到2之间。科赫曲线有一个不是整数的维度,而是分数,我们也称之为有分形维度。
分析复杂度
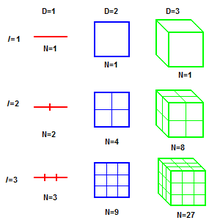
有不同的方式去衡量分形的维度,这取决于分形是如何构造的。在科赫曲线这个例子中,用到了豪斯多夫维数概念。这是分形在每一个循环中长度,面积或者体积的变化的测度。当你给一条线加上1倍,它的长度也加倍了。当你给矩形的边长加上1倍,它的面积增长了3倍。当你给立方体的边长加上1倍,它的体积增长了8倍。因此,它们的豪斯多夫维数分别是1,2,3。
创建科赫曲线时,我们需要把每一段曲线取三分之一,然后复制四份,这个过程在每一个新的线段创建时都会重复。所有的分形都用同样的循环步骤生成,根据定义,分形豪斯多夫维数等于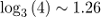 。
。

如果你有兴趣的话,维基百科有一些非常有趣的分形,点击查看。
结论
这篇文章快速简明地介绍了分形的概念,下一篇文章将会探讨为什么自然中分形出现的概率如此之大,并且它们为什么如此重要。

Comments !